Homepage > Documents > Neo-Riemannian Transformations in the Tonnetz

Triad Tonnetz and Riemannian Transformations

The Tonnetz diagram and Neo-Riemannian Theory

This page contains a link to a PDF document with Tonnetz diagram templates, which you may use for chord progression designs. Also there is a companion Riemannian Transformations booklet to the YouTube video tutorial series, and a set of full orchestral scores for the longer examples in the series.

Tonnetz Diagram >> | Riemannian Transformations >> | Tonnetz templates >> | Video tutorials >>

Introduction to the Tonnetz

The Triad Tonnetz Diagram In Neo-Riemannian Theory (NRT) we may use the Tonnetz Diagram as a graphical tool for analysing and designing chord movement. The diagram has pitch-class labels from the chromatic scale at the nodes. Sets of three connected notes yield major and minor triads.

The example Tonnetz shown in the figure is centered around the C major triad. Neighbouring triads have two overlapping, common pitches, a property used in the design of triad chord progressions. Since the chromatic scale is periodic through octave transposition, there is redundancy in the diagram and we observe double (multiple) occurrence of the triads.

Riemannian Transformations

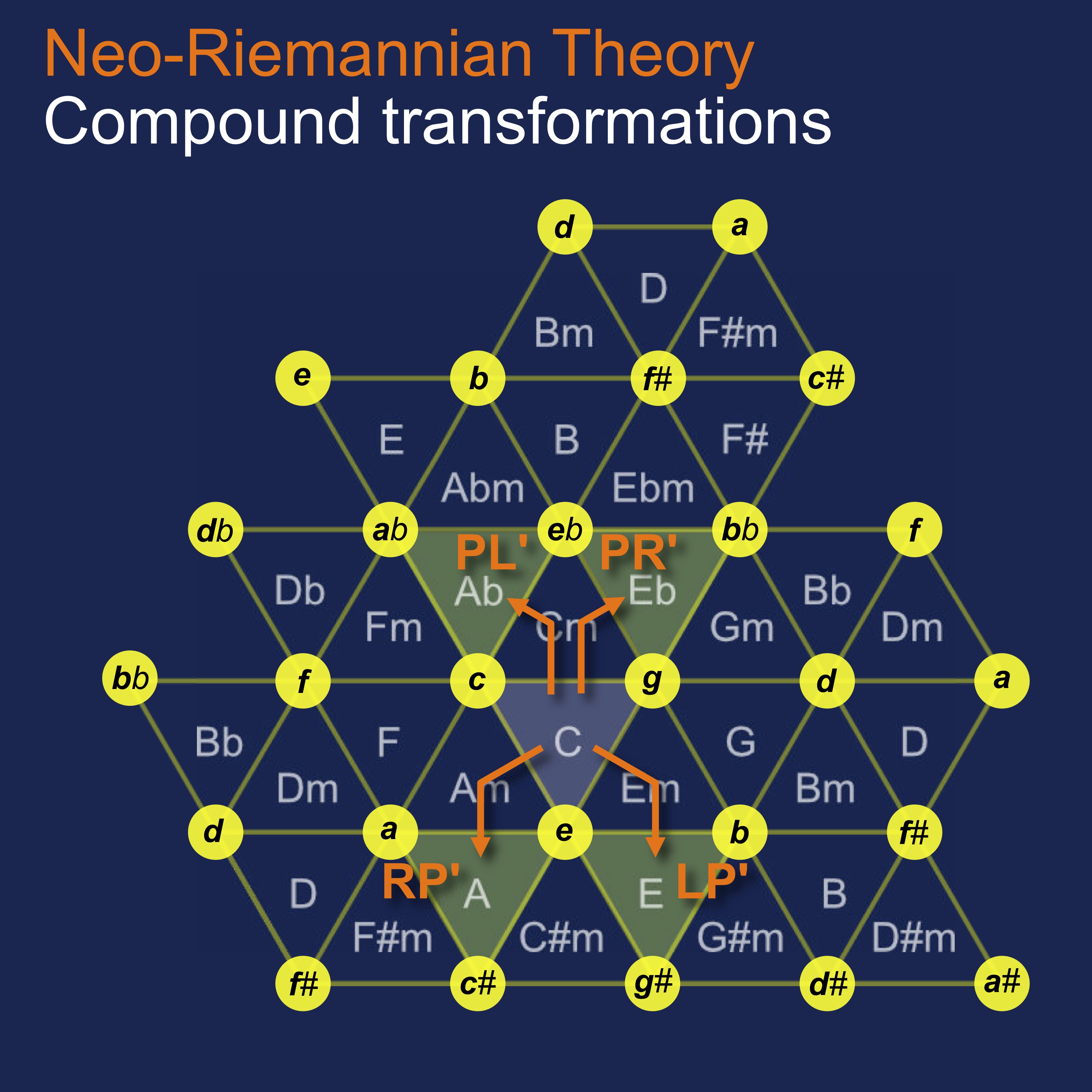Compound Riemannian Transformations in the Tonnetz In triadic chord progressions through the Tonnetz we use Riemannian Transformations. There are three basic transformations: {P,R,L}. The P transformation connects a triad with the parallel minor or major chord, e.g., going from CM (M: major triad) to Cm, or in the reverse direction. The R-transformation is the connection with the relative minor triad, such as in CM-Am (or the inverse Am-CM). The L-transformation is called the leading tone exchange, since when connecting CM-Em the latter triad contains the leading tone b from the C major diatonic 7-pitch scale.

More interesting connections are made through compound Riemannian Transformations, the pairwise combination of the basic transformations into {PR,RP,PL,LP}. These are shown in the Tonnetz diagram when starting from a major triad. The two connected triads are known as chromatic mediants since they do not occur in diatonic harmony. Used by classical music composers such as Schubert and Wagner, these 'operatic' chord connections imply a narrative value with corresponding listener emotional response, and therefore have become popular in contemporary (epic) film music.

The Tonnetz Diagram templates

If you would like to compose music cues with Riemannian transformations, use my template diagrams. The document with the Tonnetz Diagram templates is available on my Patreon page (PDF, landscape, 3 pages).

Riemannian Transformations video tutorials

On my YouTube channel I uploaded a 4-episode series of video tutorials on Riemannian Transformations in the Tonnetz. These explain the fundamentals, all basic and compound transformations and the corresponding root cycle in the Schillinger diatonic and symmetric harmony system. All transformations are demonstrated with short composition examples.

Here are the links to the YouTube video tutorials:

  1. Riemannian Transformations: Part 1 Schillinger Caught in the Tonnetz (26:59) presents the three basic and the four compound transformations with composition examples.
  2. Riemannian Transformations: Part 2 Five Paths to Domination (18:06). Simple and compound Riemannian transformations applied to a Schillinger Dominant Pedal Point chord progression framework.
  3. Riemannian Transformations: Part 3 "Order, order, order!" (26:08). Third order compound transformations.
  4. Riemannian Transformations: Part 4 The Long and Winding Tonnetz Threads (20:17). Longer chord progressions with various transformation types.

Additional documents: